How will LIBOR options transition?

Introduction

The process to transition linear derivatives (FRAs, Swaps) to a new RFR rate is now well understood. The LIBOR reference rate will be replaced by the relevant RFR rate plus a spread, as below:

The spread, x, will be decided either by using a bilaterally agreed level or, more likely, by following the method agreed in the new ISDA protocol to use an historic calculation of the 5-year median spread.

The issue of the transition of non-linear interest rate products, like options, is slightly more complicated. We can recognise this by observing that option prices are driven by more factors than just the underlying rate. For vanilla options, there are three main factors that drive the price, all of which will affect the fair transition process. They are:

·       Forward rate

·       Volatility

·       Time to expiry

Applying a swap-like transition to options, where we adjust the underlying reference rate, takes care of only one of these factors (the forward rate). As we will see, transition to a backward-looking compounded RFR rate may also affect the other two price factors.

Dealing with the underlying rate factor

Transition of the underlying rate on interest rate options, following the ISDA protocol, is relatively straight-forward.

For caps and floors, the prevailing strike on the trade would be modified by the calculated spread adjustment, as shown below using the payoff formula for a cap:

For example, if an existing LIBOR 1.0% cap versus 3m USD LIBOR is transitioned using a spread adjustment of 15 bps. The result would be a new SOFR cap with a strike of 0.85%.

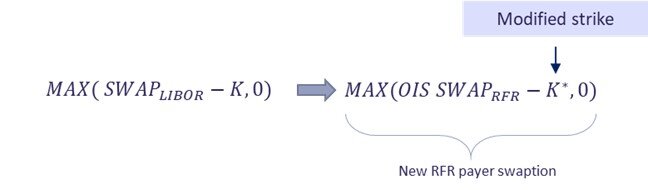
For swaptions, the same logic would apply, again shown below using the payoff formula for a payer:

The new swaption is now exercisable into an OIS swap (referencing the RFR rate), rather than a LIBOR swap.

One small point to note here is that for swaptions, the new strike, K*, would be further adjusted from the simple ‘K-x’ modification we saw with caps and floors, to account for the slightly different PV01s on the floating and fixed legs of the underlying swap (driven by the usual difference in day count conventions on each leg). However, this further adjustment will be small and uncontroversial.

The question once the reference rate has been modified is: has the value of the option changed due to other factors?

Value change due to volatility

The volatilities of RFR forwards (and OIS swaps) are not necessarily the same as the volatilities of LIBOR forwards (and swaps). This can result in value transfer on transition for an interest rate option whose underlying reference rate has been amended using the ISDA protocol.

To see this, we recognise that a forward LIBOR rate for a certain future period is a combination of two components:

[The FRA_OIS spread is known as LIBOR_OIS when discussing a spot-starting comparison.]

The volatility of a forward LIBORi will be a function of the volatilities of the two component parts, the forward RFRi rate and the forward FRA_OIS spreadi, along with the correlation between the two. Using a simple assumption that all components are normally distributed, the volatility of the forward RFRi rate will vary as per the below diagram:

The outcome of this is that if a cap or floor is transitioned by using the ISDA protocol to adjust the underlying rate (by adjusting the option’s strike), this may still result in value transfer between the counterparties if the appropriate RFR rate volatility differs from the LIBOR volatility used in the original trade.

For example, taking the 1% USD LIBOR cap from above which was transitioned using a spread of 15bps to a new SOFR cap with a 0.85% strike. If VOLSOFR < VOLLIBOR, the buyer of the cap would suffer a loss unless there was a corresponding compensation payment on transition.

For swaptions we have a similar problem for the same reason, i.e. it is likely that VOLLIBOR_SWAP ≠ VOLOIS_SWAP.

Value change due to time to expiry

The good news here is that swaptions are unaffected by this factor as they will continue to be exercised at the same point in time. For example, a 1y5y payer referencing a LIBOR swap will be transitioned to a 1y5y payer referencing an OIS swap. Both old and new trades will expire in 1y and exercise into the appropriate underlying swap if in the money.

For caps and floors though, the situation is more complicated.

Looking at an example of a single period 12m x 15m LIBOR caplet, we currently have the following:

The time to expiry on the LIBOR caplet is 12 months; driven by the time till the reset of the LIBOR rate. If we use the ISDA protocol to transition this caplet to backward-looking compounded RFR + x, then we now have the following:

Two things have happened here. Firstly, the time to expiry has increased by 3 months. Secondly, the option has become an average rate option (albeit with an averaging window and a compounded result rather than an arithmetic average). To cope with the latter, the option should now be priced (and booked) using an average rate pricing model rather than a standard Black-Scholes caplet pricing model.

From a pricing point of view, the effect of the compounding process in the last 3 months is to reduce the effective extension of the time to expiry, as even though the final rate is not known until the end date, its outcome becomes ever more certain as resets come in. This can be represented as an effective maturity extension of somewhat less than 3 months for the 12m x 15m caplet, as shown below:

The outcome on caps and floors is therefore twofold.

1.     Value transfer will occur due to this factor, always from the seller to the buyer, because of the increase in the time value of the option as the result of the extension in the equivalent time to expiry.

2.     Newly transitioned caps and floors should be booked using average rate pricing models which allow for the calculation of a backward-looking compounded rate and therefore produce the correct risk metrics.

Conclusion

We have examined the effect of using the ISDA protocol to transition vanilla LIBOR interest rate options to new RFR options. We have seen that value transfer can occur between buyer and seller, once the underlying LIBOR rate has been modified, due to two remaining factors:

·       For both caps/floors and swaptions, the volatility used on the original LIBOR trade may not be appropriate for the new RFR trade, potentially resulting in value transfer between buyer and seller.

·       Caps and floors will have an effective extension to their time to expiry, resulting in an increase in time value and a value transfer from seller to buyer.

It may be that there is an offsetting effect due to the above two factors. For example, if the RFR cap/floor volatility is lower, this would, at least partially, offset the increase in time value due to the maturity extension. This offsetting effect would not apply to swaptions which are exposed only to the volatility change.

A full analysis should be done of the impact of both factors on the valuation of your interest rate options portfolio in order to be certain of the magnitude of any value transfer, and hence the requirement for compensation payments on transition.

FMCR is a specialist technical consultancy firm with experience in interest rate risk management products and can provide consultancy services on all aspects of LIBOR transition and financial risk management.